Tip of the Day 149: The Mystery of the “Integral” (part 2)

With an understanding of what an integral IS, the popular next question is “How do you compute it? I know how to figure the area of a rectangle or triangle but what is formula for the area of this:  ?”

Answer: Let the eDART™ calculate it.

Those with an itch to know more, read on.

To find the area of a shape that has no formula we simply break it into small areas that do have formulas: in this case a series of thin rectangles. Back to the property metaphor: Walk the road and mark every 100 yards with your GPS. Then walk the river and read out distances to the road at each GPS longitude line, breaking the property into 11 parts like this:

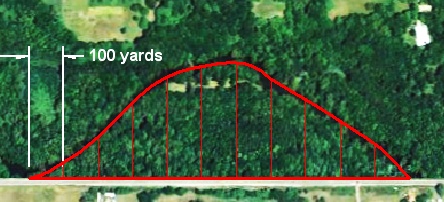
Each slice is averaged into a rectangle^† shown here in blue (just one height given as an example):

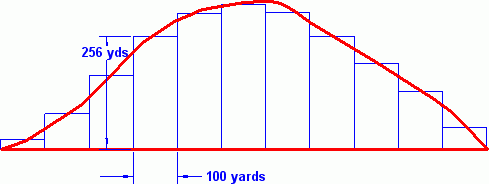
Then we can calculate the area of each rectangle as width (100 yards) x height. We add those 11 areas and come up with something close to the area of under the curve.



You will, of course, say “That’s pretty sloppy!” Quite so. So why not use 10 yard steps giving us 110 rectangles? Still not accurate enough? One yard, then? ^‡

The eDART only makes rectangles as thin as its sample rate in time steps. “Time” is the road in the property example. This is quite adequate for creating stable values that correlate to dimensions and weights.

Next Tip (# 150 ): Why do integrals have weird units (psi-sec.) and huge numbers (50,000 +)?

^†Making Rectangles from Trapezoids

Standard numerical integration methods get the best accuracy for the selected step size by averaging the two sides of each rectangle to come up with one height like this (using the same slice as in blue above):

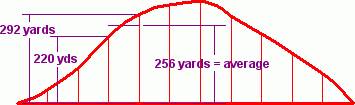
The average of 292 and 220 is 256 which comes from (292 + 220) ÷ 2

This is the same thing as calculating the area of each rectangle under the curve and adding the area of each little triangle on top thus (the triangles are hatched for emphasis):

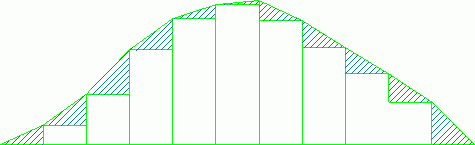
The first method gives good results using the lowest computing time. With a little algebra the computing time can be reduced even further.

^‡ Isaac Newton got the idea to make the rectangles infinitely thin, thus inventing The Calculus (“The” was required by my physics prof.).